A crash course on asset allocation
· 1202 words · 6 minutes read
In previous posts, I talked about passive investing and its Belgium-specific matters. I will now discuss asset allocation, which is one of the most important topics in investing. It’ll be more of a theoretical post but I will elaborate on some core principles that I think are important.
Why asset allocation?
In many situations in life, it’s wise to not put all your eggs in one basket. The same holds for investing. That is what asset allocation is about: choosing the right mix of securities in your portfolio in order to reduce risk while maintaining a high expected return.
Markowitz’s insight
Markowitz is the father of Modern Portfolio Theory. One of his important insights was the following:
A mixture of volatile noncorrelated securities results in a portfolio with lower volatility and potentially higher return.
This may seem counter-intuitive at first so I will try to illustrate with an example. We will first look at the lower volatility part and then at the potentially higher return.
Lower volatility through diversification
First of all, lower volatility is a good thing because a highly volatile investment is also very risky. And as investors, we want to keep risks low. An investment that has a lower risk but an equal expected return is a better investment.
Imagine that there are two stocks A and B, whose returns over 4 years are as in the following table.
| Stocks | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|
| Stock A | 50% | -25% | 50% | -25% |
| Stock B | -25% | 50% | -25% | 50% |
For example, after the first year, stock A gains 50% while stock B loses 50%.
Let’s say that we have $1000 to invest. We are going to compare three portfolios:
- 100% stock A
- 50% stock A, 50% stock B: we buy $500 worth of each stock at the start and maintain those stocks during all four years.
- 100% stock B
The following table shows the returns of each portfolio over these 4 years.
| Portfolios | Year 0 | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|---|
| 100% stock A | $1000 | $1500 | $1125 | $1688 | $1266 |
| 50% stock A, 50% stock B | $1000 | $1125 | $1125 | $1266 | $1266 |
| 100% stock B | $1000 | $750 | $1125 | $844 | $1266 |
You can see that the total return after 4 years is the same for all portfolios: a good 27% gain. However, when you look at the intermediate returns, it seems that portfolio 2 exhibits a lot less variation. It stays between $1000 and $1266 whereas the other portfolios reach much higher and lower levels. To confirm this suspicion, we compute the standard deviation of each portfolio:
| Portfolios | Standard deviation |
|---|---|
| 100% stock A | 279 |
| 50% stock A, 50% stock B | 112 |
| 100% stock B | 208 |
As the standard deviation is a measure for the volatility, we can conclude that the mixed portfolio is less risky. We achieved the same return for a less risky investment meaning that objectively, the mixed portfolio is the better investment. This illustrates the first part of Markowitz’s insight.
Higher returns through rebalancing
By diversifying our portfolio across the two stocks, we lowered its volatility and therefore the risk associated with our investment. However, we haven’t made any additional returns with this strategy. Whether we invested it all in stock A or a mix of stock A and B, we are stuck with a profit of $266.
This is where rebalancing can bring extra returns. With rebalancing, we regularly buying and selling stocks so that our initial allocation is maintained.
In our mixed portfolio, we start with $500 worth of each stock. After 1 year, the value of the stock A portion has grown to $750 (50% growth) whereas the stock B part has decreased to $375. So our allocation has changed to 67% stock A and 33% stock B, which is far from our wanted allocation. Therefore, we sell $187.50 of stock A and buy the same amount of stock B. This brings us back to our 50% allocation.
What is the impact of rebalancing?
| 50% stock A, 50% stock B | Year 0 | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|---|
| no rebalancing | $1000 | $1125 | $1125 | $1266 | $1266 |
| with rebalancing | $1000 | $1125 | $1266 | $1424 | $1602 |
That’s a big difference! By simply rebalancing ever year, our return jumps from 27% to 60%. And this without taking on any additional risk.
The intuition behind rebalancing is that it forces us to sell when a stock is high and buy when it’s low. Rebalancing works because prices that are low tend to go back up (eventually) and high prices will likely come down at some point.
The impact of correlation
There’s a third factor that we haven’t looked at and that is correlation. Markowitz’s insight says that the securities in our portfolio should be uncorrelated. What does that mean and why is this the case?
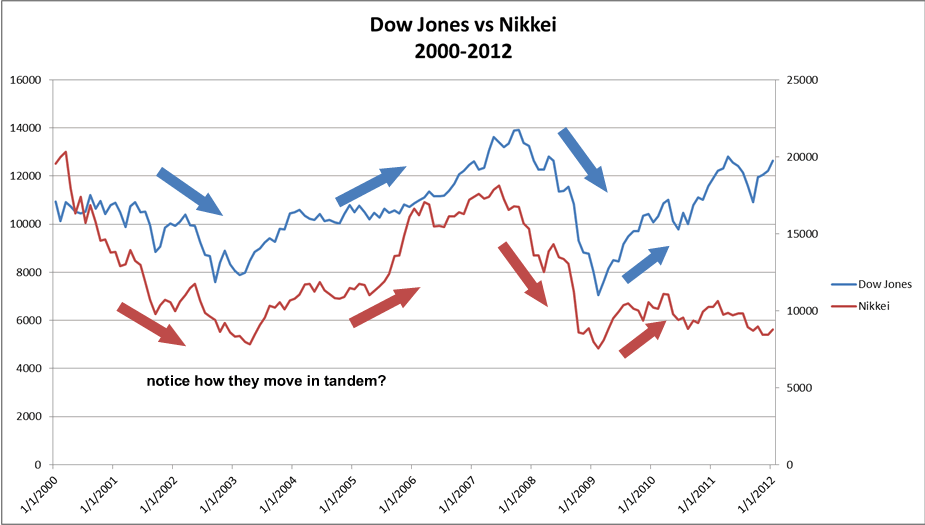
Two securities are positively correlated when they move together. For instance, the Nikkei and the Dow Jones are clearly correlated as can be seen below. In other words, when the US economy goes up, the Japanese economy goes up again, and vice versa.
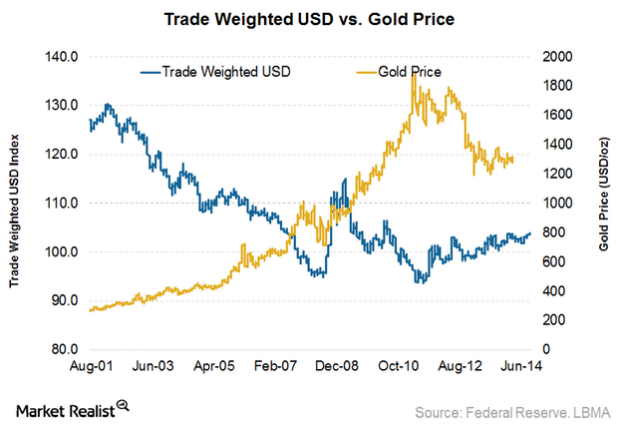
In contrast, the USD and gold are negatively correlated. When the price of gold goes down, the value of the USD tends to go up, and vice versa.
In our example, stock A and stock B were negatively correlated. Indeed, the years that stock A went up, stock B went down. What would happen if our portfolio instead consisted or stocks that were more positively correlated?
Let’s do a similar simulation but with the following stocks:
| Stocks | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|
| Stock A | 50% | -25% | 50% | -25% |
| Stock B | 40% | -20% | 40% | -20% |
The returns (without rebalancing):
| Portfolios | Year 0 | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|---|
| 100% stock A | $1000 | $1500 | $1125 | $1688 | $1266 |
| 50% stock A, 50% stock B | $1000 | $1450 | $1123 | $1628 | $1260 |
| 100% stock B | $1000 | $1400 | $1120 | $1568 | $1254 |
What interests us is the standard deviation:
| Portfolios | Standard deviation |
|---|---|
| 100% stock A | 279 |
| 50% stock A, 50% stock B | 224 |
| 100% stock B | 251 |
The standard deviation of the mixed portfolio went up from 112 to 224! This means that by diversifying, we have hardly lowered the risk. This means that we’re gaining a lot less from diversifying when the stocks in our portfolio are positively correlated.
Does it also negatively impact our return when rebalancing?
| 50% stock A, 50% stock B | Year 0 | Year 1 | Year 2 | Year 3 | Year 4 |
|---|---|---|---|---|---|
| no rebalancing | $1000 | $1450 | $1123 | $1628 | $1260 |
| with rebalancing | $1000 | $1450 | $1124 | $1629 | $1263 |
We only gain an additional 0.3% return when rebalancing as opposed to 33% in the previous situation. This shows that when creating a portfolio, its securities should be as negatively correlated as possible.
Recap
This was a short summary of what I find the most important principles behind asset allocation. In a nutshell, this is what we learned:
- To reduce volatility (and therefore risk), it is important to compose a diversified portfolio of securities.
- Volatility is reduced most when the securities in your porfolio are negatively correlated.
- Rebalancing can greatly increase the return of your portfolio.
I plan on covering my own portfolio in a future post so it will get more practical then!